Joint Orientation Statistics

If you are performing a Probabilistic Analysis with RocSlope2, the Joint Orientations can be defined as random variables as follows:

1. Select Home > Joints > Orientations
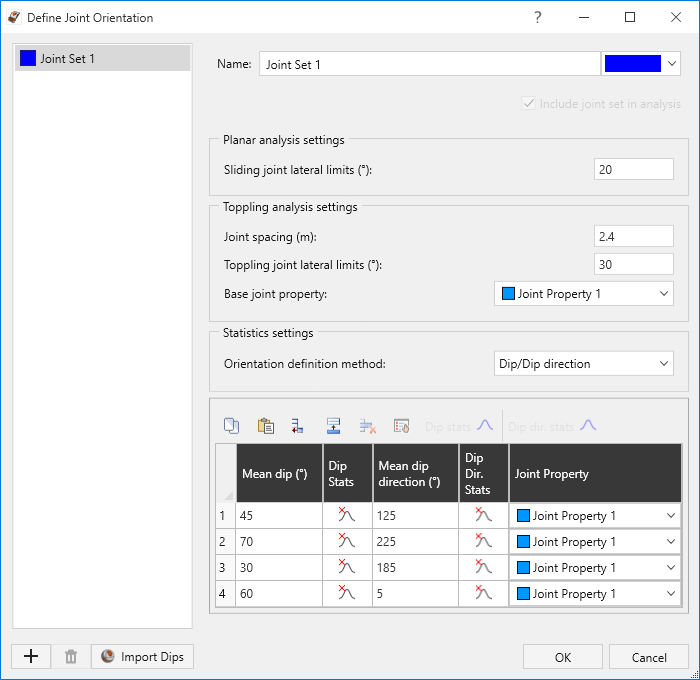
2. Under the Statistics Settings, select an Orientation Definition Method. There are two methods of defining the variability of Joint Orientation in RocSlope2:
   • Dip / Dip Direction
   • Fisher

See below for information about these options.

3. Enter or import the Joint mean orientation and statistical parameters as described below.
   

Dip / Dip Direction

If the Orientation Definition Method = Dip / Dip Direction, then the Dip and Dip Direction of a Joint can each be assigned a statistical distribution and are treated as independent random variables (i.e. during the statistical sampling, there is no correlation between the generated values of Dip and Dip Direction).

The Dip / Dip Direction option allows you the flexibility to choose any two distributions for the Dip and Dip Direction of each Joint. This can be useful if the actual distribution of orientations you are trying to model is asymmetric (e.g. an elliptical distribution on the stereonet). However, if your orientation distribution is approximately circular, then you should use the Fisher option.

Fisher Distribution

If the Orientation Definition Method = Fisher, then the Joint orientations will be randomly generated according to a Fisher Distribution. A Fisher Distribution assumes a symmetric distribution of 3-dimensional orientations around the mean, and only requires a single parameter (Fisher K value or standard deviation) to define the variability of the distribution.

See the Fisher Distribution topic for more information.

Import from Dips

You can import the Joint mean orientation and Fisher K value from a Dips *.dwp, by selecting the Import from Dips button and selecting the desired joint set from a Dips *.dwp file.

See the Import from Dips topic for more information.

Comparison of Dip / Dip Direction and Fisher Distribution Methods

The following figures illustrate an example of the difference between the two methods of generating random plane orientations in RocSlope2.

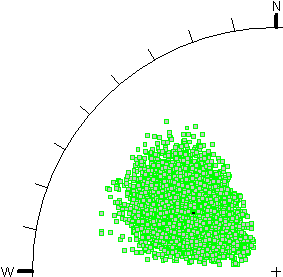
• In Figure A, the Dip and Dip Direction are specified as independent random variables, using a Normal distribution and a standard deviation of 10 degrees for both dip and dip direction.
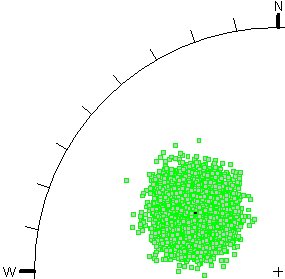
• In Figure B, a Fisher Distribution is used, with a standard deviation of 10 degrees.

In both cases, 10,000 random plane orientations were generated. The stereonet projection method is Equal Angle.

As you can see, the Fisher Distribution results in an approximately circular distribution of orientations (poles) around the mean orientation (on an Equal Angle stereonet projection). The Dip/Dip Direction method results in an asymmetric oval-shaped distribution of poles, for the given input parameters.

The advantage of the Fisher distribution is the ability to produce a symmetric distribution of orientations around the mean orientation, for 3-dimensional orientation data, regardless of the direction of the mean orientation. In general, the Fisher distribution is recommended over the Dip/Dip Direction (two-variable) approach, because the data input is simpler, and the results are more reliable [Meyers and Priest (2000)].

If your actual joint set pole distribution is asymmetric, then you can use the Dip/Dip Direction method to specify independent distributions for the Dip and Dip Direction.