Joint Property Statistics

If you are performing a Probabilistic Analysis with Rocslope2, the following Joint Properties can be defined as Random Variables:

• Strength
• Waviness Angle
• Water Parameters

Strength

If you are performing a Probabilistic Analysis with RocSlope2, the Joint Strength can be defined as a Random Variable, as follows:

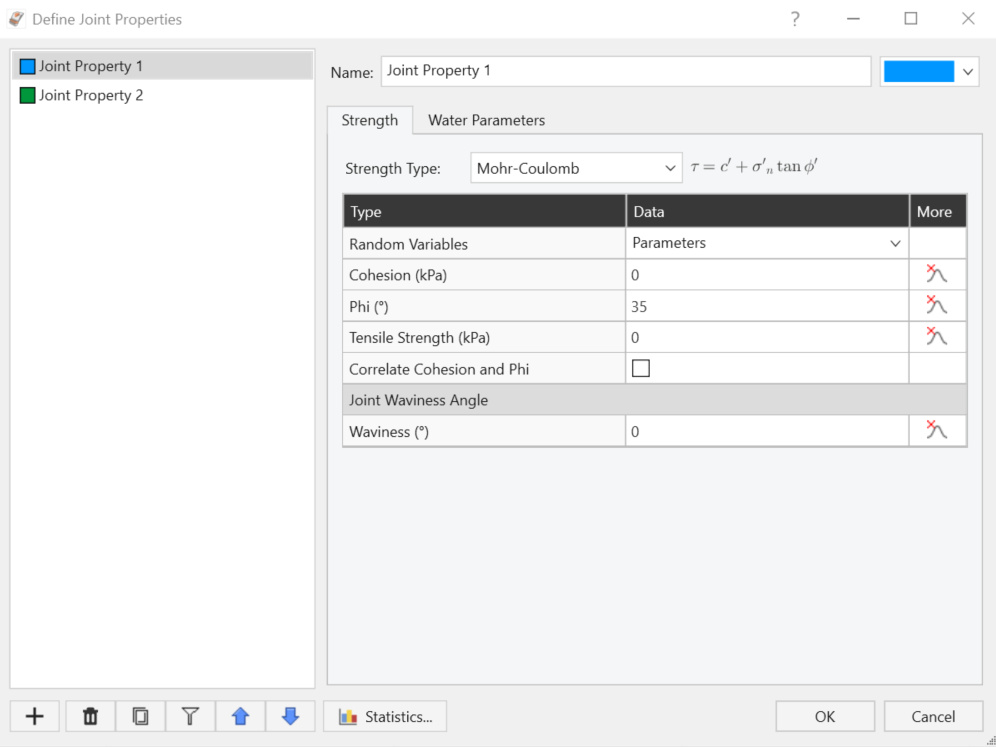
1. Select Home > Joints > Properties
2. Select the desired Joint Property from the left-side pane
3. Under the Strength tab, select the Strength Type (Mohr-Coulomb, Barton-Bandis or Power Curve).
4. There are two different methods of defining Strength Random Variables in RocSlope2:
   • Parameters
   • Strength



See below for information about these options.

Random Variables: Parameters

If Random Variables = Parameters, then you can define a Statistical Distribution for each parameter used in the strength criterion (i.e. Cohesion, Phi, and Tensile Strength for Mohr-Coulomb; JRC, JCS, and Phir for Barton-Bandis; a, b, c, d for Power Curve).

Correlation Coefficient

If you are using the Mohr-Coulomb strength model, then you can define a correlation coefficient between cohesion and friction angle by checking Correlate Cohesion and Phi. See the Correlation Coefficient topic for details.

If you are using the Barton-Bandis or Power Curve strength models, then you can NOT define the correlation between the statistical sampling of the strength parameters (i.e. the statistical sampling of each parameter is performed independently of the sampling of any other random variables).

Random Variables: Strength

If Random Variables = Strength, then the shear strength (tau) is defined directly as a random variable, rather than defining the individual parameters of the strength criterion as random variables. For a given normal stress, a random value of shear strength will be generated. This works as follows:

1. Set Random Variables= Strength.
2. Choose a statistical distribution for the shear strength. Only Lognormal and Gamma distributions are allowed, because these distributions are only defined for positive values, and therefore ensure that randomly generated values of shear strength will always be positive.
3. Enter the Coefficient of Variation for the shear strength. The Coefficient of Variation is equal to the standard deviation divided by the mean shear strength.
   
   CV = s_{τ /} m_τ or s_τ = CV (m_τ)
   
   where CV = coefficient of variation of shear strength.
   
   s_τ = standard deviation of shear strength.
   
   m_τ = mean shear strength.
   
Typical values of shear strength CV range from 0.15 to 0.35 [Miller et.al. (2000)].
4. Enter the mean values of the strength criterion parameters (e.g. cohesion and friction angle for the Mohr-Coulomb criterion).
   
5. When the probabilistic RocSlope2 analysis is computed, random values of shear strength are generated as follows:
   • The normal stress on a joint plane is computed.
   • Using the mean values of the strength criterion parameters (e.g. cohesion and friction angle), the mean shear strength is calculated. This defines a point on the mean strength envelope.
   • Using the mean shear strength, coefficient of variation, and the selected statistical distribution (Lognormal or Gamma), a random value of shear strength is generated, for the given normal stress. This will be the actual value of shear strength used in the RocSlope2 safety factor calculation.
   • The above steps are repeated for each probabilistic simulation until the required number of samples are generated.

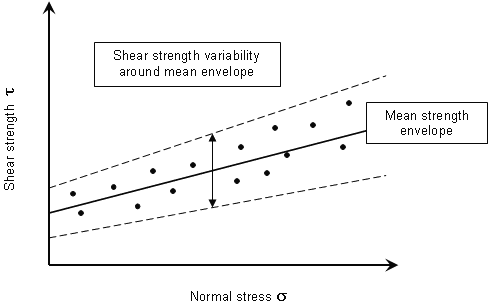
The random shear strength option is schematically illustrated in the following figure, for the Mohr-Coulomb criterion. Essentially, you are defining a variability of shear strength about the mean strength envelope. This is intuitively simpler to grasp than defining variability of individual strength parameters.

The random shear strength option is particularly useful for Barton-Bandis or Power Curve strength models since it eliminates the need for defining statistical distributions for individual strength parameters (which may be difficult to obtain or unavailable). Furthermore, the issue of statistical correlation of the strength parameters is avoided (i.e. you do not have to worry about generating unrealistic combinations of strength parameters, since variability is defined with respect to the mean envelope).