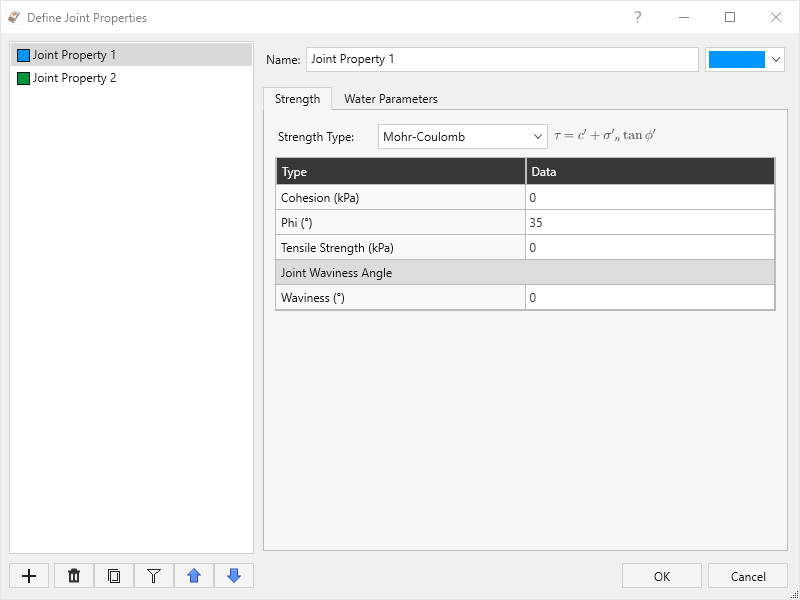
Shear Strength

The shear strength of the joint planes in RocSlope2 can be modelled using any of the following strength criteria:

• Mohr-Coulomb
• Barton-Bandis
• Power Curve

To define a joint’s shear strength:

1. Select Home > Joints > Properties
2. The Define Joint Properties dialog will open. Select the Joint Property you would like to edit using the left-side menu.
3. Select the Strength tab in the main dialog area.
4. Choose the Strength Type (Mohr-Coulomb, Barton-Bandis, or Power Curve) and enter the joint strength parameters.

• For a Deterministic Analysis, define the shear strength of a Joint Property to be applied to a single joint set or multiple joint sets, including Basal Joint Set (if enabled).
• For a Probabilistic Analysis, it is possible to define statistical variability of the joint strength properties. See the Joint Property Statistics topic for more information.

The shear strength models are described below.

Mohr-Coulomb

The Mohr-Coulomb model relates shear strength, τ, and normal stress σ_n, according to Eqn.1:

τ= c + σ_n tan ϕ + σ_n tan ϕ_w

where:

𝝉 = shear strength

c = cohesion

𝝓 = friction angle

Barton-Bandis

The original Barton equation for the shear strength of a rock joint is given by Eqn.2:

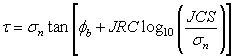
Where 𝝓_b is the basic friction angle of the failure surface, JRC is the joint roughness coefficient, and JCS is the joint wall compressive strength [Barton, 1973, 1976]. On the basis of direct shear test results for 130 samples of variably weathered rock joints, this was later revised to Eqn.3:

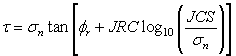
Where 𝝓_r is the residual friction angle of the failure surface [Barton and Choubey, 1977]. Barton and Choubey suggest that 𝝓_r can be estimated from Eqn.4:

ϕ_r = (ϕ_b - 20) + 20 (r / R)

Where r is the Schmidt hammer rebound number on wet and weathered fracture surfaces and R is the Schmidt rebound number on dry unweathered sawn surfaces. Equations 3 and 4 have become part of the Barton-Bandis criterion for rock joint strength and deformability [Barton and Bandis, 1990].

For further information on the shear strength of discontinuities, including a discussion of the Barton-Bandis failure criterion parameters, see this Practical Rock Engineering resource (Chapter 4: Shear Strength of Discontinuities).

Power Curve

The Power Curve model for shear-strength [Miller, 1988], can be expressed as:

τ = c + a (σ_n + d)^b

Where a, b and c are parameters typically obtained from a least-squares regression fit of data obtained from small-scale shear tests. The d parameter represents the tensile strength. If included, it must be entered as a positive value.