Spline Search

1.0 Introduction

The stability of a slope is governed by the critical slip surface, which corresponds to the lowest factor of safety. In this tutorial you will learn to use some of the advanced searching methods, such as Spline Search, offered in Slide3 on a coal mine example.

Generally, the process of searching for the critical slip surface involves trying different shapes such as spheres and ellipsoids to cut the ground topography. The sliding mass above the cut is discretized into soil columns and its internal forces are solved for static equilibrium to determine the factor of safety (FS). Scaled, rotated, and translated variations of these shapes are used to minimize the value of FS obtained in the sliding mass.

The Spline Search is a powerful feature original to Slide3 which uses spline-based surfaces in 3D which are varied to determine the critical slip surface. As demonstrated in this tutorial, it is generally more effective at predicting the FS than ellipsoid or spherical searching.

The completed tutorial file is Spline search – final file.slide3m2, which can be found in File > Recent Folders > Tutorials Folder.

2.0 Initial Model Setup

Start the Slide3 program. For this tutorial, go to File > Recent Folders > Tutorials Folder and choose Spline search – starting file.slide3m2.

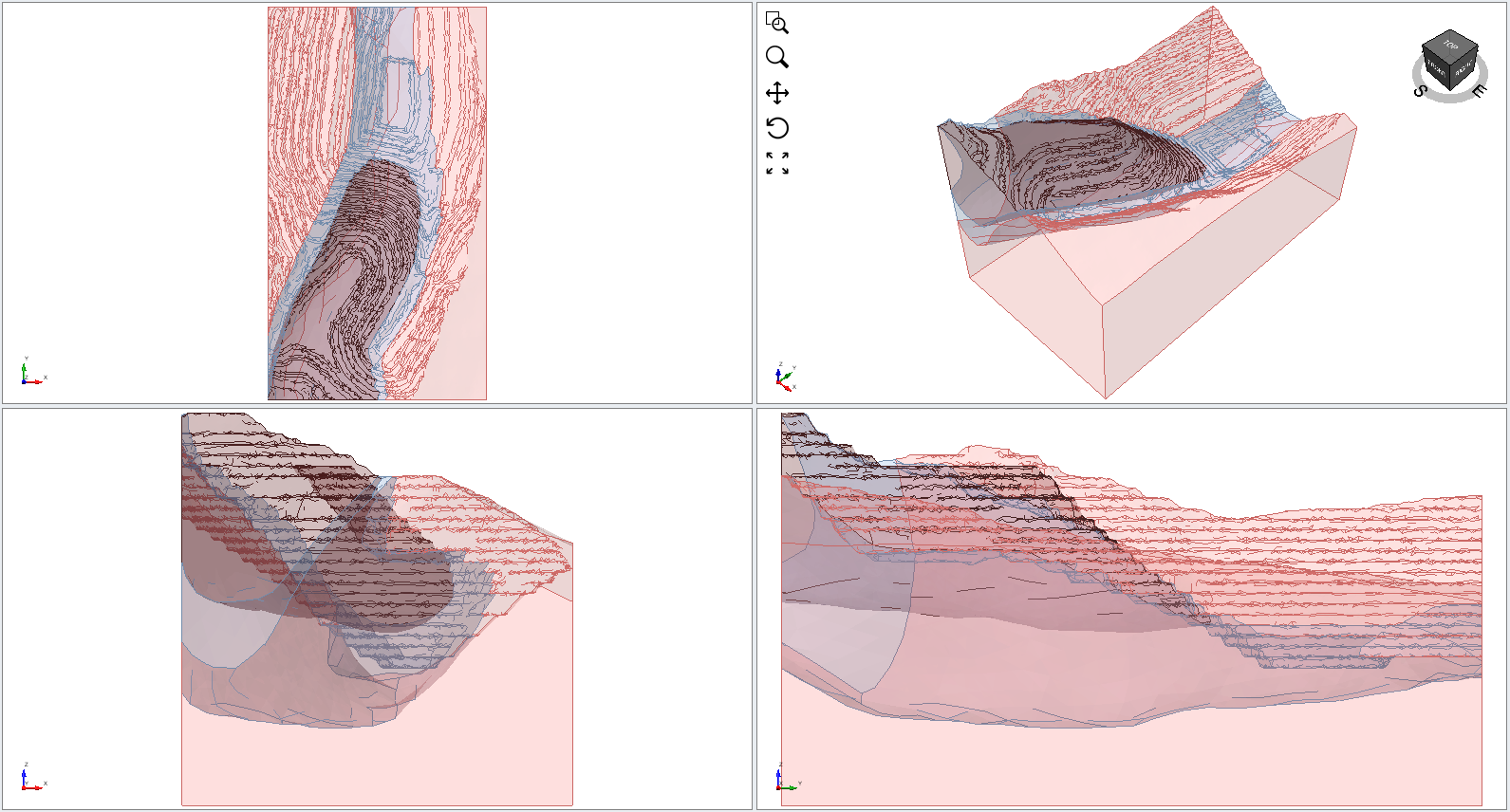
2.1 Surface Options

1. Go to Surfaces > Slip Surface Options.
2. Ensure that Ellipsoid search is selected, with using Cuckoo Search.
3. Ensure that the Surface Altering Optimization checkbox is OFF.
4. Click OK to close the dialog.

2.2 Compute

1. Save the model by selecting File > Save As in the menu. Be sure to name it something different so you don’t overwrite the starting file for this tutorial.
2. Select Analysis > Compute in the menu to perform the analysis. Depending on your computer’s speed, this may take up to a few minutes.

2.3 Results

When the computation is finished, the results will automatically be displayed. The Bishop FS obtained by the Ellipsoids search in this example is close to 2.1.

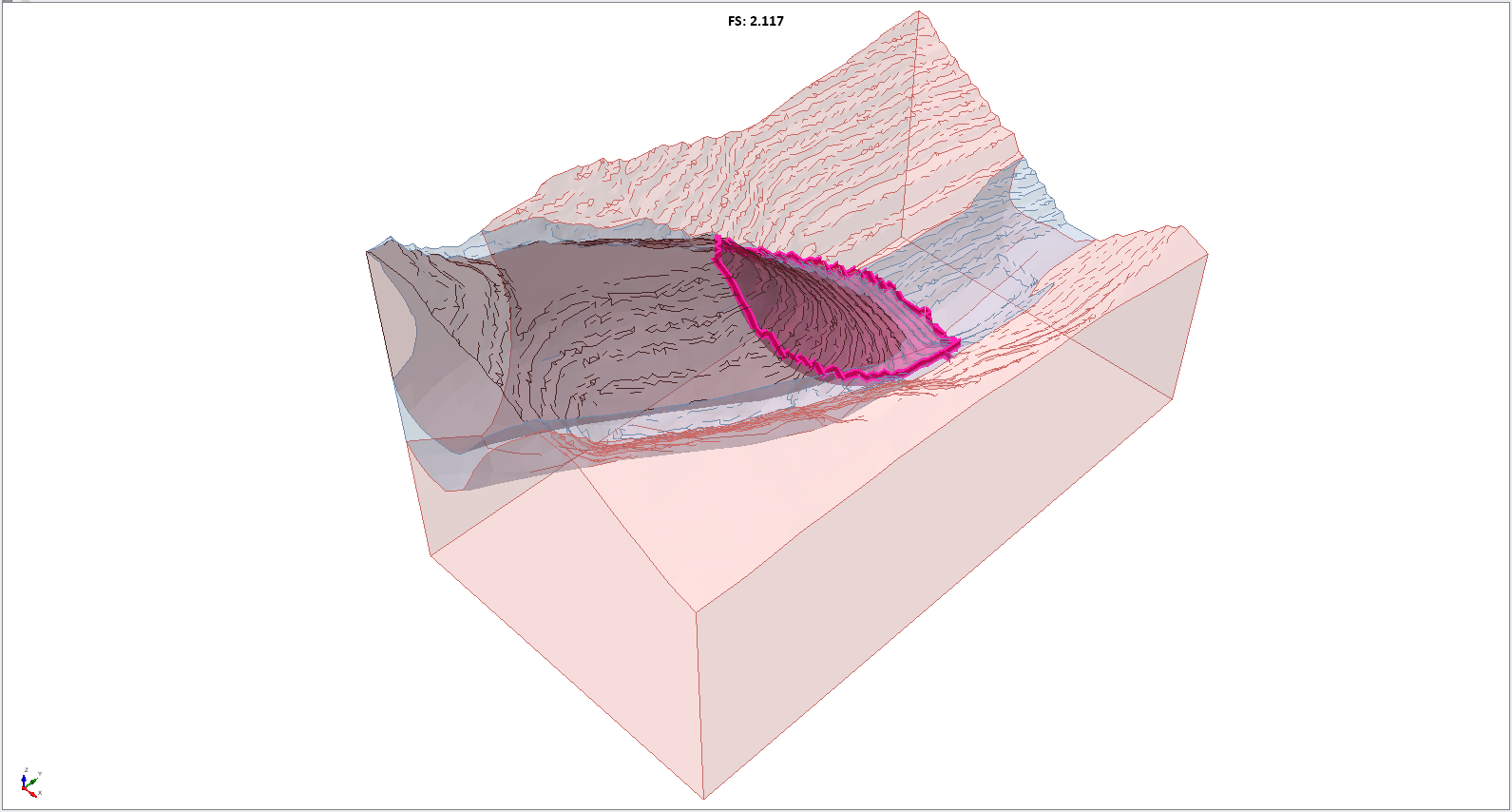
Click on Interpret > Show All Surfaces. You can use this to see a composite of the outlines of slip surfaces generated during the search process.

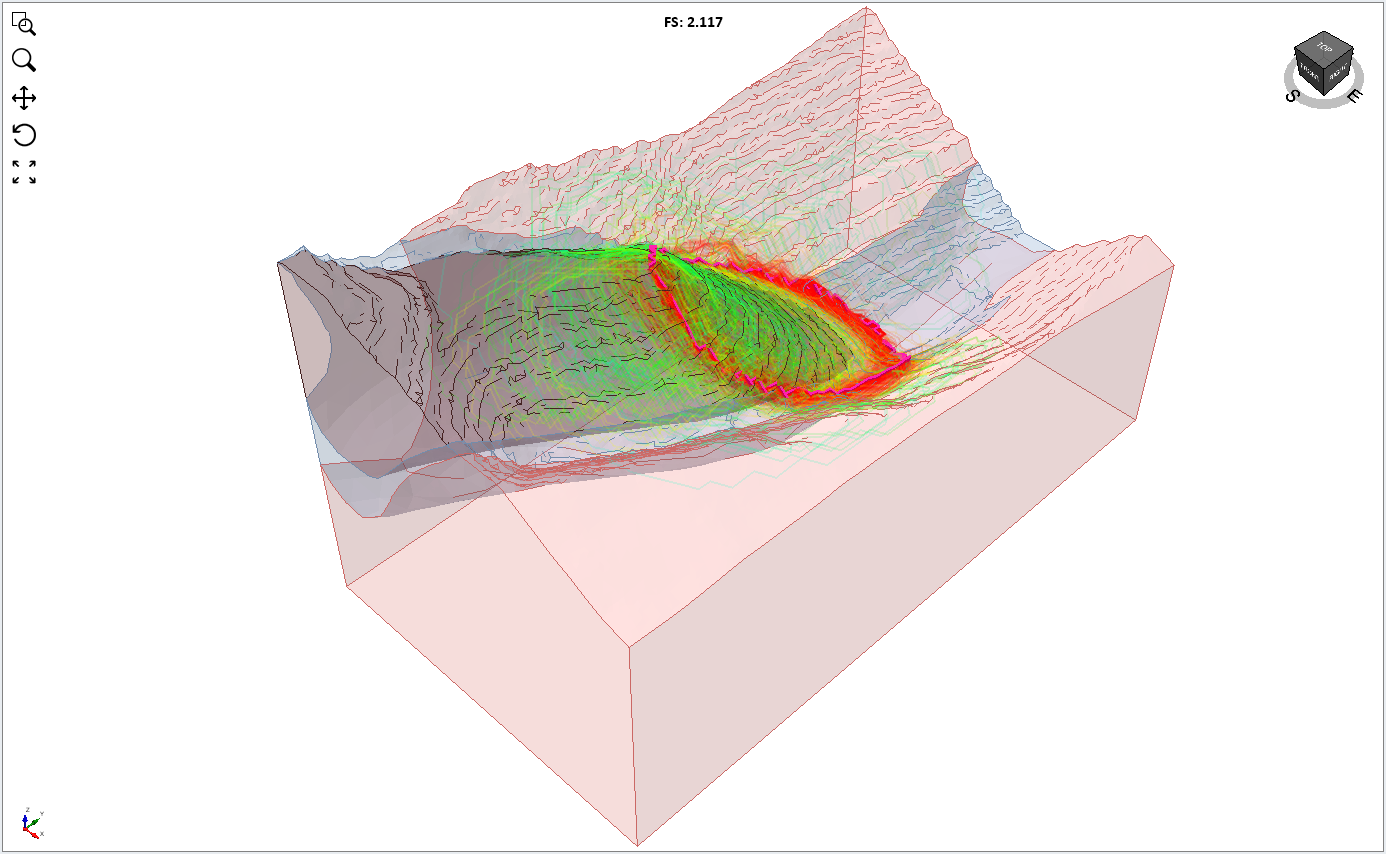
It is important to note that if the model is too large, there may be inadequate coverage of searching throughout the model. In such cases, we recommend using the Search Limits tool to focus the searching on areas of interest via Surfaces > Add Search Limit, and/or to increase the number of iterations via Surfaces > Slip Surface Options > Options.

3.0 Improving the Search

You will notice that all the generated surfaces in the previous results are ellipsoidal. We now point out that as slip surfaces are seldom ellipsoidal or spherical in real life, the ellipsoidal search by itself may not always produce the true factor of safety in a slope.

To better predict the true FS for this slope we will incrementally employ a combination of the more powerful Spline Search Method and Surface Altering Optimization methods.

3.1 Spline Search

Spline search uses 3D Spline surfaces consisting of weighted control points to cut the ground topography. The shape of the curves in the spline surface are more flexible than for ellipsoids because the relative locations of the points in the spline can be varied during the search.

1. Select Surfaces > Slip Surface Options.
2. Change the surface type from Ellipsoid to Spline.
3. For now, do NOT change the search method, and do NOT select the surface altering optimization option.
4. Click OK to close the dialog.
5. Save the model.
6. Select Analysis > Compute in the menu to run the modified analysis.

When the computation is finished, the updated results will automatically be displayed. The Bishop FS obtained by the Spline search this time is about 2, which is less than the ellipsoidal search.

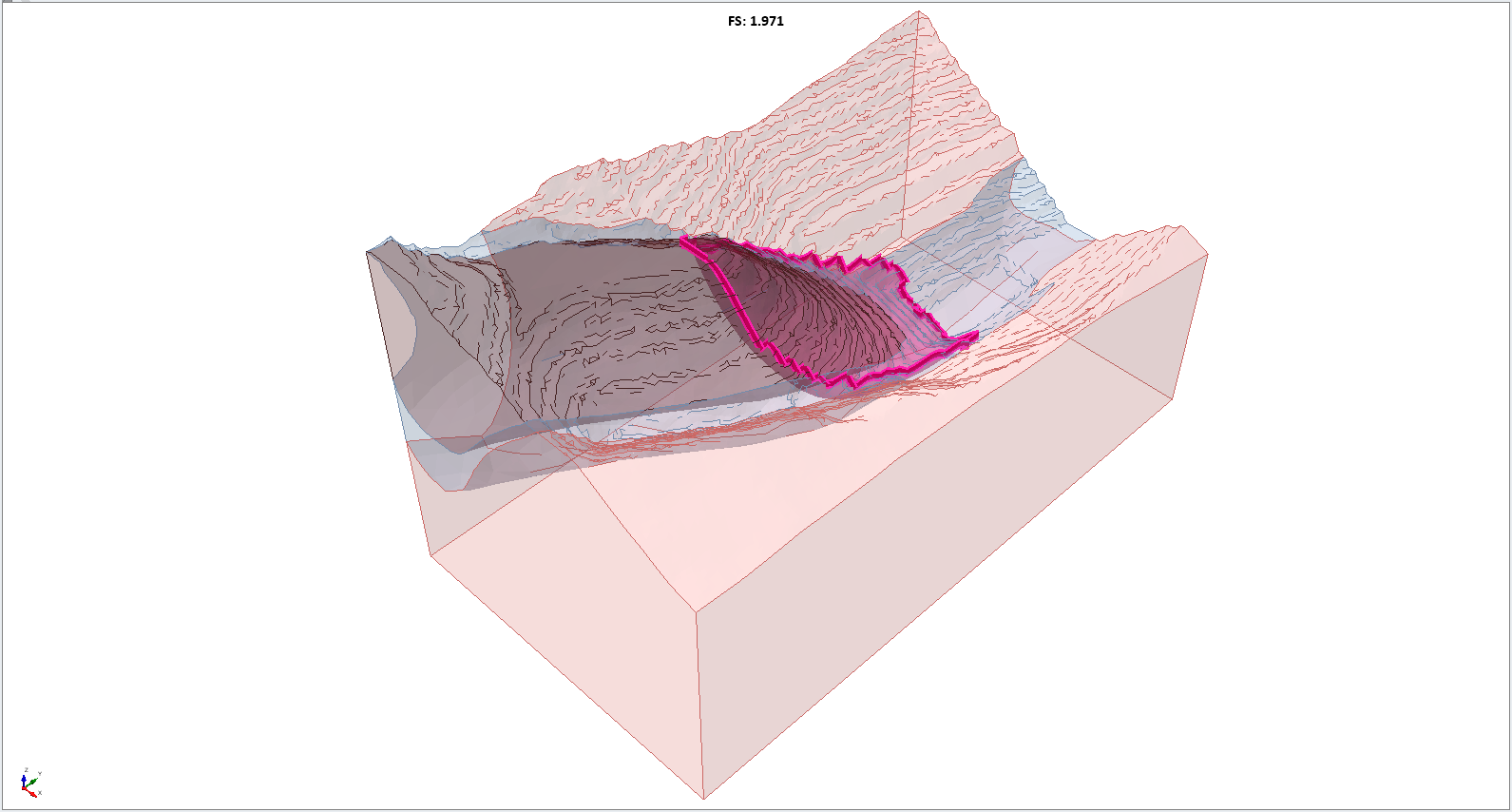
3.2 Particle Swarm

An alternative to Cuckoo Search is the Particle Swarm search, which performs similarly to Cuckoo Search but requires fewer function evaluations given the same number of iterations and is therefore more efficient. Both methods are Swarm Intelligence methods which rely on a degree of random heuristic methods inspired by nature to efficiently find the minimum FS.

1. Select Surfaces > Slip Surface Options.
2. Change the Search Method from Cuckoo Search to Particle Swarm Search.
3. Do NOT change any other options in the dialog, and then click OK.
4. Select Analysis > Compute in the menu to run the modified analysis.

Notice that the computation is completed significantly faster using PSO, despite having the same number of iterations. The Bishop FS obtained this time is close to 2.0, which is an improvement compared to the ellipsoidal search and Cuckoo Search.

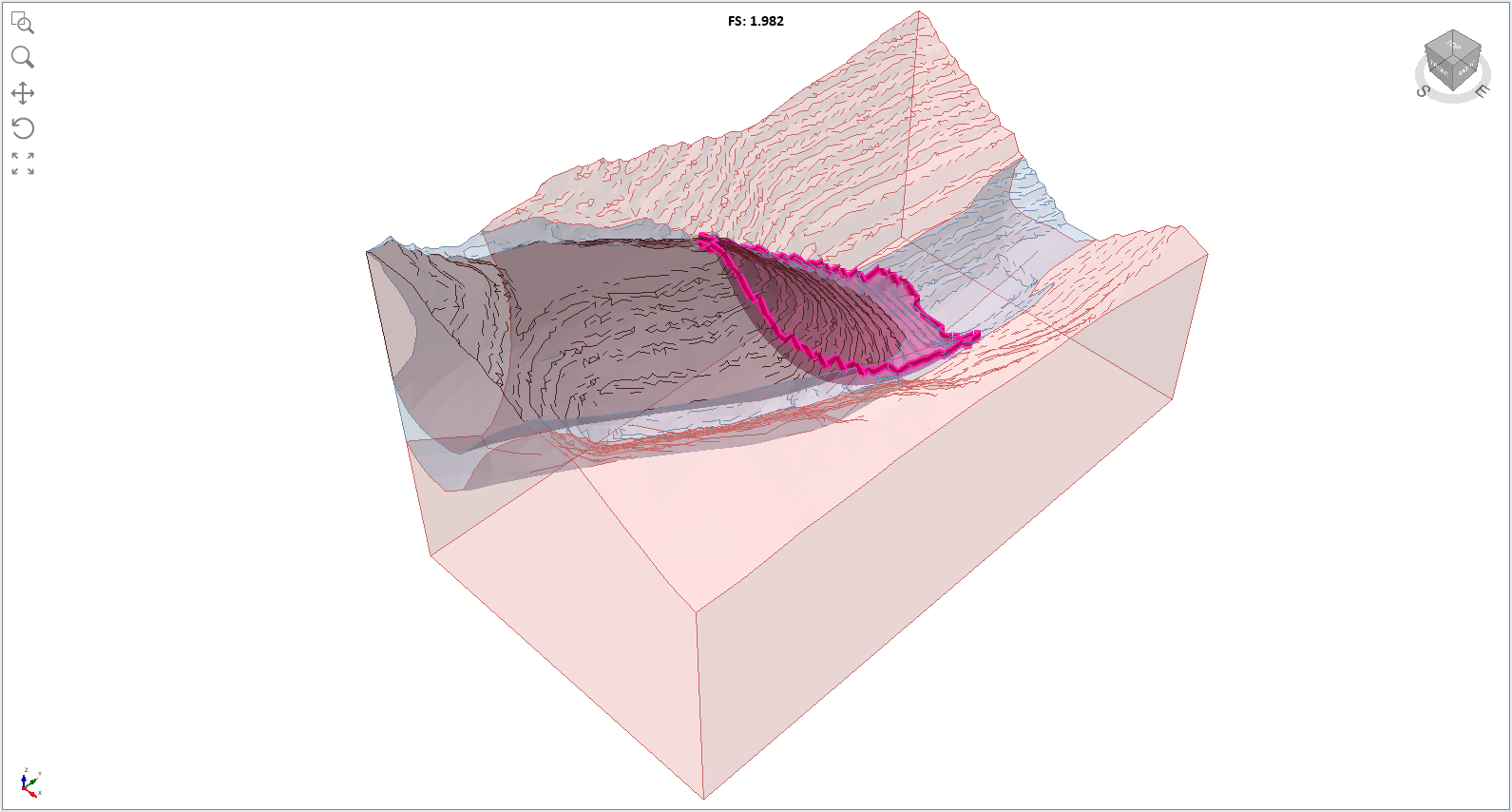
3.3 Surface Altering

Although the spline search is more flexible than the ellipsoid search, the coarseness of the searching is still on a global scale, as it primarily aims to identify the general region of the model with the lowest FS. It is recommended to further locally optimize the minimum spline surface using the Surface Altering Optimization option via the following steps.

1. Select Surfaces > Slip Surface Options.
2. Activate the checkbox Surface Altering Optimization.
3. Do NOT change any other options in the dialog, and then click OK.
4. Select Analysis > Compute in the menu to run the modified analysis.

Note: There are some additional options that one can use to fine-tune the surface altering process, which are described here.

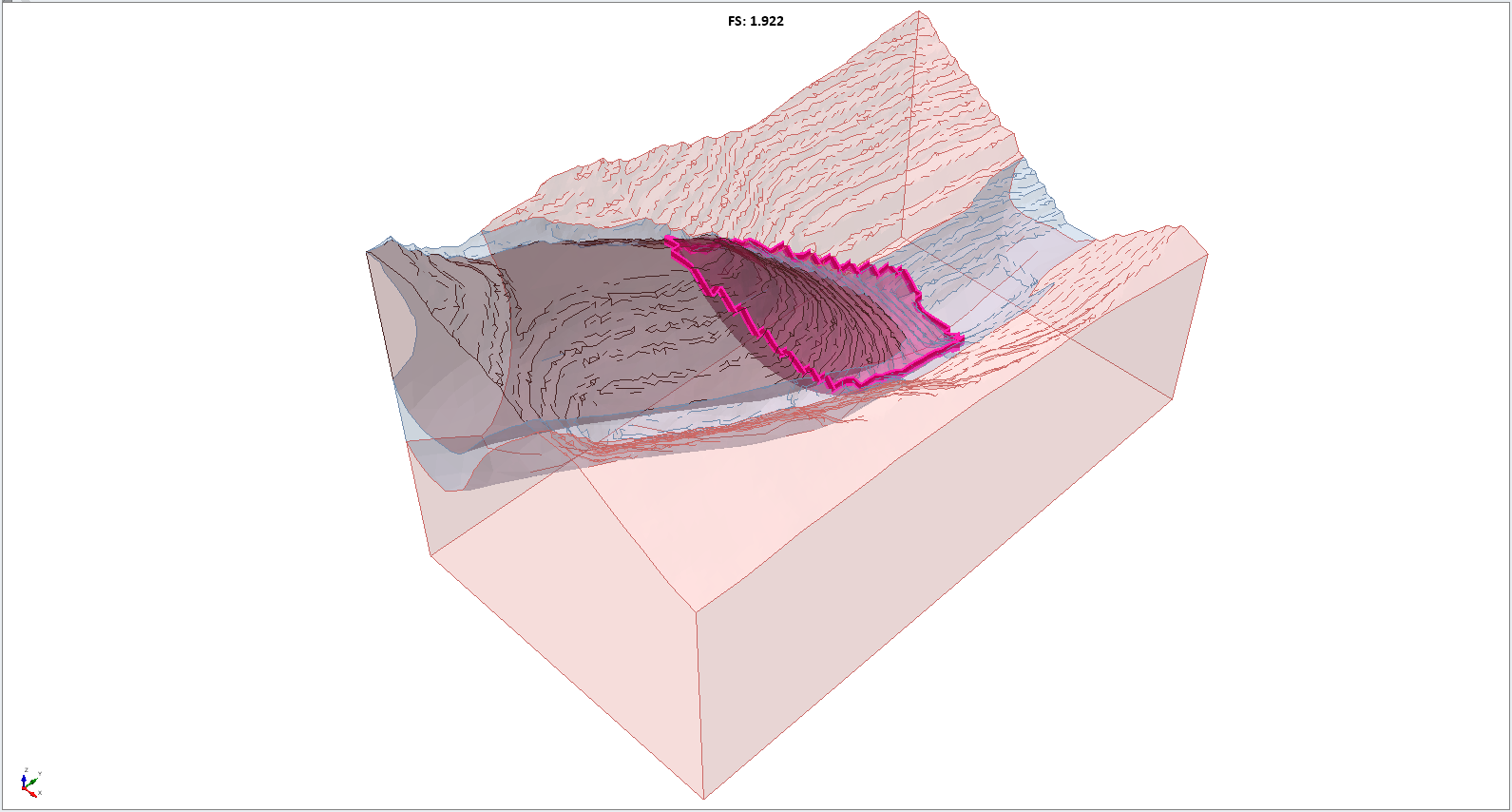
The final FS is below 2.0, representing a moderate improvement from that obtained from just the spline search, and a significant improvement form the result obtained from ellipsoid search.

4. References

Full details of the spline search and surface altering algorithms, along with a detailed text on the geometry of NURBS surfaces can be found in the following publications:

Ma, T., Cami, B., Javankhoshdel, J., Corkum, B., and Yacoub, T. (2022). Optimization of spline slip surfaces using metaheuristic search in LEM. In Proceedings of the TMIC2022 Slope Stability Conference, Atlantis Press (Springer Nature). https://www.atlantis-press.com/proceedings/tmic-22/125984717

Ma, T., Mafi, R., Cami, B., Javankhoshdel, S., and Gandomi, A.H. (2022). NURBS surface-altering optimization for identifying critical slip surfaces in 3D slopes, Int J. Geomech, 22(9): 04022154.

Piegl, L., Tiller, W. (1997). The NURBS Book, Springer-Verlag Berlin, Heidelberg.