Facilitating Geotechnical Engineering Problems Using Metaheuristic Optimization Algorithms
By Ali R. Kashani, University of Memphis, and Amir H. Gandomi, University of Technology Sydney
The main concern in numerical modeling of every real-world phenomenon follows two fundamental approaches: 1) meeting the minimum requirements to reach the demanding serviceability and 2) finding the best choice among tons of possibilities. Although the first approach has been resolved by developing a wide range of commercial software, the second remains challenging.
Recently, soft computing techniques have been used to handle a wide variety of complex problems. Among them, metaheuristic optimization algorithms have addressed the second approach efficiently. Whether the task is one of maximization of minimization, the problem with every level of complexity can be handled successfully using an appropriate metaheuristic optimization algorithm.
It should be noted that the performance of these metaheuristic algorithms can be affected to a considerable extent by complex optimization tasks that are discontinuous, non-convex, and nonlinear with multiple local minima. Geotechnical problems are considered to be complex because of multivariable dependencies of soil responses and uncertain behavior of soils. In addition, a large number of independent variables are required to describe a given phenomenon. Therefore, there are many cases in which the objective function is non-convex and discontinuous with lots of strong local minima within their solution domain.
This article looks at the application of metaheuristic optimization algorithms for facilitating four complex geotechnical problems: 1) slope stability analysis, 2) optimum design of concrete cantilever retaining walls, 3) optimum design of shallow foundations, and 4) minimization of reinforcement lengths in mechanically stabilized earth.
Problem 1 – Slope Stability Analysis
In this case, the complex geotechnical problem is accounted for by a non-homogenous soil slope in which a weak soil layer is sandwiched between two stronger layers. The failure surface in this kind of soil slope is non-circular and slips over the weak soil layer.
In this problem, the objective function is nonconvex and discontinuous with multiple strong local minima, so the metaheuristic optimization algorithms are highly likely to be trapped in those local minima. Many studies have therefore been conducted to determine the ability of different algorithms to handle this sort of problem. In this article, we consider one of the most complicated cases that were subject to a large number of studies.
The profile of the soil layers and the different slip surfaces are depicted in Figure 1 and results are compared in Table 1 (Gandomi et. al., 2015a and 2017a; Kashani et. al., 2016), where GA is Genetic Algorithm, PSO is Particle Swarm Optimization, DE is Differential Evolution, ES is Evolutionary Strategy, BBO is Biogeography-Based Optimization, FA is Firefly Algorithm, CS is Cuckoo Search, LKH is Levy-flight Krill Herd, and ICA is Imperialistic Competitive Algorithm.
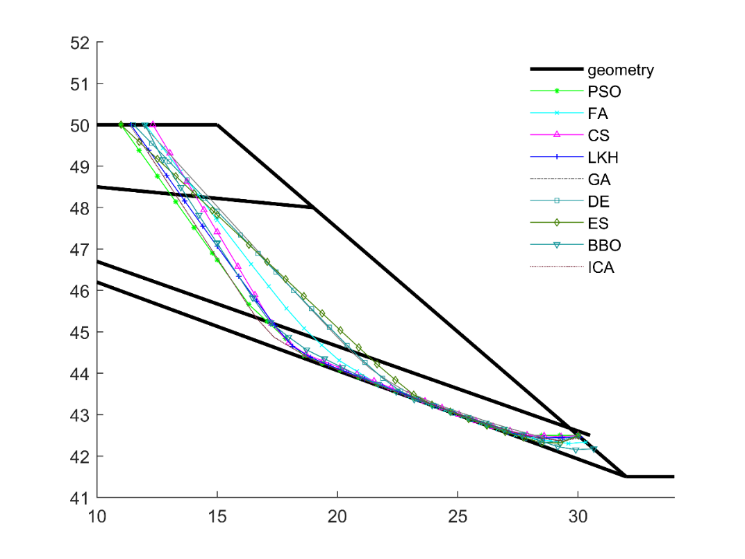
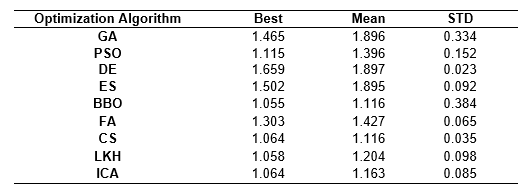
As shown by the results, the range of factor of safety (FOS) values obtained by the different algorithms varies between 1.659 and 1.055. The FOS value of 1.659 can be seen to represent a high level of stability for the tackled slope while 1.055 can be considered the marginal FOS for this slope. An accurate analysis of a given slope is therefore crucial to the determination of stability of a slope.
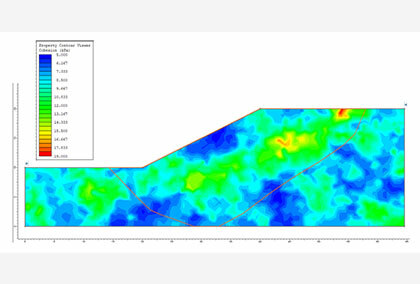
Figure 2 shows results of the same problem modeled using Rocscience’s Slide2 software (Rocscience 2018).
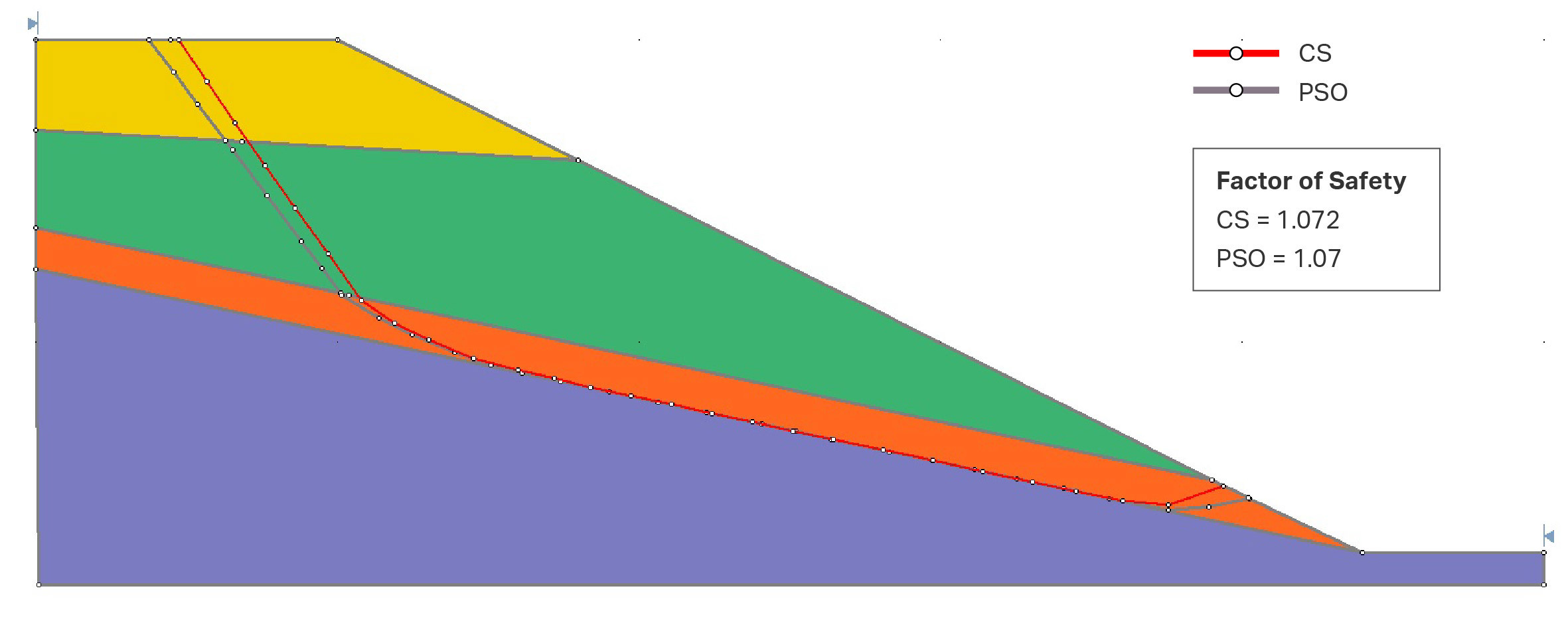
In the Slide2 model, Cuckoo Search (CS) and Particle Swarm Optimization (PSO) search methods were used to find the critical slip surface together with the Spencer Limit Equilibrium Method (LEM). A local optimization technique called Surface Altering Optimization (SAO) was also used to better search for the critical slip surface. SAO is a novel approach to minimizing the FOS for a given slip surface using spline curves in 2D. It is a local search algorithm that, combined with a global search method such as CS or PSO, can form a powerful hybrid optimization technique used in slope stability analysis.
The FOS values computed using Slide2 are 1.072 for CS and 1.07 for PSO. The values are slightly lower than those presented for the matching methods in Table 1, which is accounted for by the additional step of finding the critical slip surface using the SAO technique. In addition, the failure surfaces in the Slide2 model compare with those for the matching methods shown in Figure 1.
Problem 2 – Optimum Design of a Retaining Wall
A retaining wall is a structure used to enhance the stability of earth masses that are unstable in their natural slopes. An appropriate design should be able to meet both the geotechnical stability and structural strength criteria simultaneously. The design procedure is defined as a minimum-cost or minimum-weight objective function in which the design variables define the geometry and number of reinforcements, as shown in Figure 3.
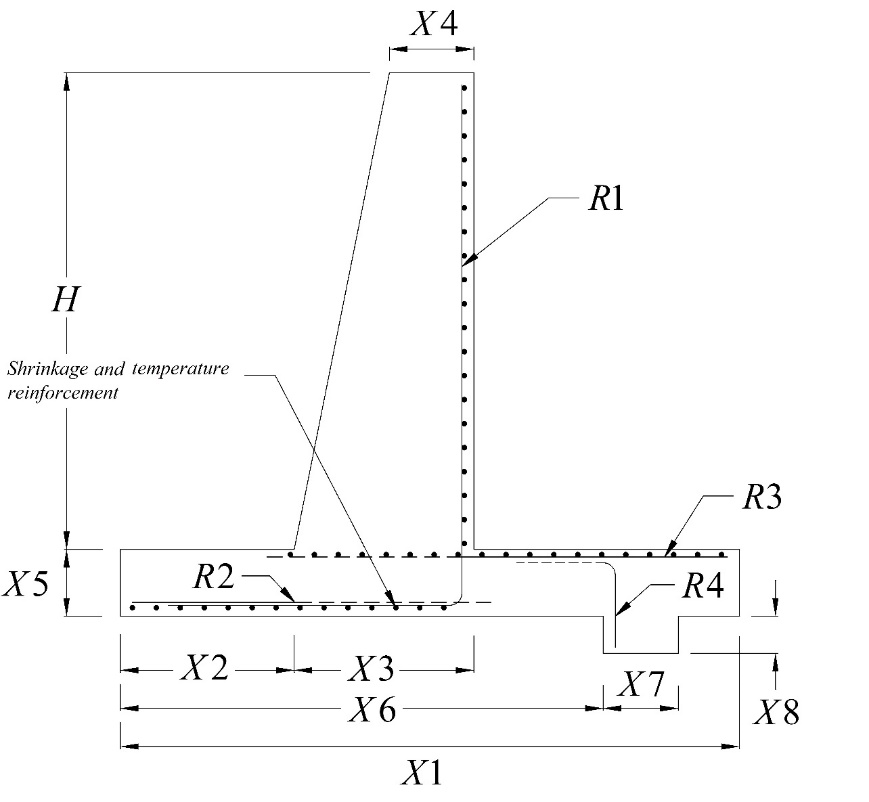
Geotechnical and structural criteria applied to the design procedure have a number of constraints. For this article, a wall 4.5 m tall with a base shear key was analyzed for both minimum-cost and minimum-weight designs, and the problem was solved using two different categories of optimization algorithm: evolutionary-based algorithms (Gandomi et. al., 2017b) and swarm-intelligence algorithms (Gandomi et. al., 2015b). The resulting low-cost and low-weight design values are presented in Table 2, where APSO is Accelerated Particle Swarm Optimization. As shown, variations in the cost and weight design among the different optimization algorithms were 12.25% and 7.6%, respectively.
Problem 3 – Optimum Design of Shallow Foundations
Shallow footing is one of the most critical structural elements that play a pivotal role in the stability of a structure. No matter the strength of a structure, its true functioning can be ruined unless a well-designed foundation directs the effective load to the earth. In order for the footing to reach impeccable performance, both geotechnical stability and structural strength requirements should be satisfied.
The objective function in this problem depends on the geometry, the position of the column at the top of the foundation, and the number and size of the reinforcements, as demonstrated in Figure 4.
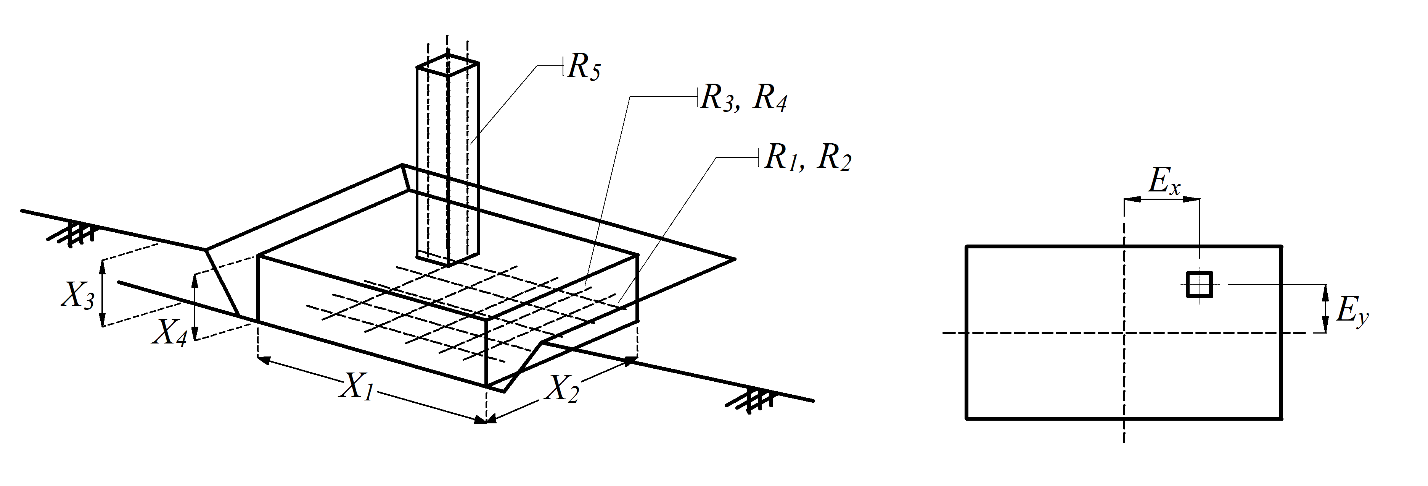
Here, we consider a shallow foundation that is affected by a combination of uniaxial load and moment. The uniaxial force results from dead and live loads of 650 kN and 350 kN, and the moment is obtained by combining dead and live load of 400 kN.m and 150 kN.m. Minimum-cost design values are provided in Table 3 based on a study by Gandomi and Kashani (2018), where WOA is Whale Optimization Algorithm, ALO is Antlion Optimization Algorithm, GWO is Grey Wolf Optimizer, MFO is Moth-Flame Optimization, and TLBO is Teaching-Learning-Based Optimization algorithm.
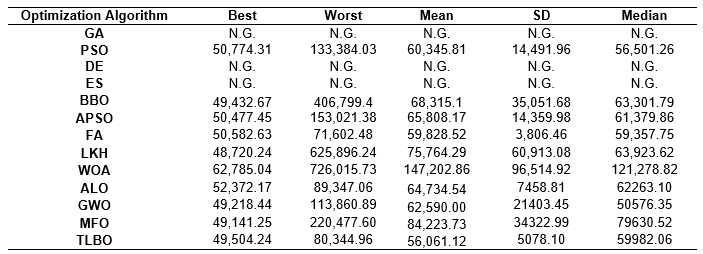
As can be seen in the table, some of the algorithms were not capable of converging to the final results, which attests to the high complexity of this problem. The range of cost values vary between $48,720.24 and $62,785.04 (22.4%).
Problem 4 – Optimum Design of Reinforced Earth Retaining Walls
The final problem tackles the minimum-cost design of reinforced earth retaining walls using metaheuristic optimization algorithms. In addition to being easy and quick to construct and install, this type of retaining structure is advantageous in very special environmental situations such as humid climate, poor foundation, and seismically active zones. It is therefore crucial for these walls to be designed accurately. Similar to the case in the first three problems, mechanically stabilized earth (MSE) must be able to provide both geotechnical stability and internal strength to endure applied forces and preserve its functioning.
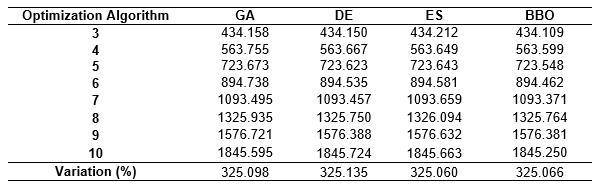
For the problem, MSE walls with geotextile were considered, and the construction costs were defined in terms of the length of the reinforcements and their vertical spaces. Trenches with heights of 3 m to 10 m with an increment of 1 m were considered as numerical simulations. Final costs are presented in Table 4. As can be seen, increasing the height of the wall from 3 m to 10 m resulted in a variation of about 325% in the cost of the wall.
Conclusion
This article explores the application of optimization algorithms to four complex geotechnical problems.
In the first problem, slope stability was analyzed using nine optimization algorithms. The results demonstrate that the evaluated FOS varies considerably due to the high complexity of the problem (between 1.659 and 1.055). This considerable variation proves that any error in this regard can result in a catastrophic disaster. The numerical examples also demonstrate the significant impact that metaheuristic algorithms have on the handling of this problem.
In the second problem, a retaining wall is considered as another complex geotechnical problem that deals with many input parameters and several limitations in the form of constraints. The final cost and weight results varied from one algorithm to another, with variations of 12.25% and 7.6% for final cost and weight, respectively. Taking into account the huge volume of these structures, it can be seen that selecting an appropriate algorithm for handling the problem can result in huge savings in construction costs.
The third problem tackled the problem of shallow foundations. Results show that, due to the complexity of the problem, some algorithms were not capable of finding a valid optimal solution that could also meet the constraints. In this case, the variation in design cost values was about 22%.
The fourth and final problem tackled mechanically stabilized earth walls. As can be seen, increasing the height of the wall from 3 m to 10 m resulted in a variation of about 325% in the cost of the wall.
References
Gandomi, A. H., Kashani, A. R., Mousavi, M., & Jalalvandi, M. (2015a). Slope stability analyzing using recent swarm intelligence techniques. International Journal for Numerical and Analytical Methods in Geomechanics, 39(3), 295-309.
Gandomi, A. H., Kashani, A. R., Roke, D. A., & Mousavi, M. (2015b). Optimization of retaining wall design using recent swarm intelligence techniques. Engineering Structures, 103, 72-84.
Kashani, A. R., Gandomi, A. H., & Mousavi, M. (2016). Imperialistic competitive algorithm: a metaheuristic algorithm for locating the critical slip surface in 2-dimensional soil slopes. Geoscience Frontiers, 7(1), 83-89.
Gandomi, A. H., Kashani, A. R., Mousavi, M., & Jalalvandi, M. (2017a). Slope stability analysis using evolutionary optimization techniques. International Journal for Numerical and Analytical Methods in Geomechanics, 41(2), 251-264.
Gandomi, A. H., Kashani, A. R., Roke, D. A., & Mousavi, M. (2017b). Optimization of retaining wall design using evolutionary algorithms. Structural and Multidisciplinary Optimization, 55(3), 809-825.
Gandomi, A. H., & Kashani, A. R. (2018). Construction cost minimization of shallow foundation using recent swarm intelligence techniques. IEEE Transactions on Industrial Informatics, 14(3), 1099-1106.
Rocscience Inc. 2018. Slide Version 2018 – 2D Limit Equilibrium Slope Stability Analysis. www.rocscience.com. Toronto, Ontario, Canada.